What is the Area of Parallelogram?

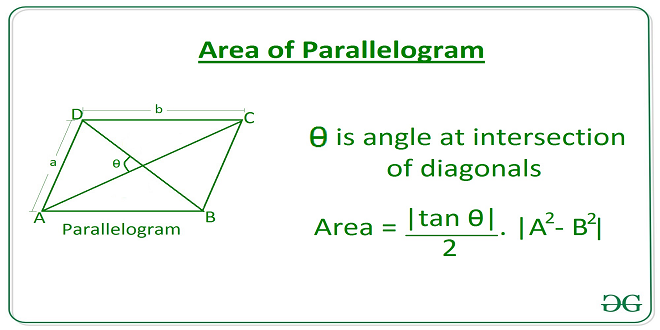
A parallelogram is a quadrilateral having four sides where two opposite sides are equal and parallel to each other. The area of a parallelogram is the space enclosed by the four sides of a parallelogram. It is measured in square units. The area of the parallelogram can be obtained by multiplying the base length and its height. The base of the parallelogram represents the horizontal bottom side and the height of the parallelogram is the distance between the bottom and topsides. The height of the parallelogram is perpendicular to the base. For parallelograms other than rectangular and squares, the lateral side of the parallelogram is not perpendicular to the base. In this case, a dotted line represents the height. You can learn this topic in Cuemath in a detailed manner.

Consider a parallelogram having a base of length ‘x’ units and the height is ‘h’ units. Then the area of the parallelogram will be as follows:

Area of parallelogram = Base of parallelogram × Height of parallelogram = (x* h) square units

For example, if the base of a parallelogram is equal to 12 cm and the height is 7 cm, then its area will be calculated as A = 12 cm x 7 cm = 84 square cm.

The rectangle satisfies the properties of a parallelogram so the area of a rectangle is calculated the same way as a parallelogram which is the product of base (the length of rectangle) and height (the width of rectangle). So the area of a rectangular parallelogram with length ‘a’ and width ‘b’ is calculated as A = a* b square units. A parallelogram in which all four sides are equal is called a square. If m is the length of each side of a square, then its area will be A = m * m square units.

What is a Parallelogram?

A geometrical figure formed by four sides is called a quadrilateral. The parallelogram is a type of quadrilateral in which the opposite or facing sides are of equal length and parallel to each other. The four angles formed by the adjacent sides are such that opposite angles are also equal to each other. The name ‘parallelogram’ originates from the Greek word that means bounded by parallel lines. So, as the name suggests, a parallelogram is a quadrilateral that is formed by parallel lines. 

Consider a parallelogram PQRS. Therefore, sides PQ and RS are parallel and equal in length which means PQ ‖ RS and PQ = RS. Again sides PS and QR are parallel and equal in length. So PS ‖ QR and PS = QR. Again, the opposite angles ∠PQR = ∠RSP and ∠SPQ = ∠QRS. For a parallelogram, the sum of same-side angles is equal to 180 degrees so ∠PQR + ∠SPQ =180 and ∠RSP + ∠QRS = 180 degrees.

Parallelograms can be of different types and named as rectangle, square, and rhombus depending upon some specific properties which are explained as follows:

• Rectangle:  A rectangle is a parallelogram with two pairs of sides that are equal and parallel and all four angles are right angles or 90 degrees.
• Square: A square is a parallelogram in which all four sides are equal in length and all four angles are right angles. 

• Rhombus: A rhombus is a parallelogram having four equal sides, but neither of the angles is right angles.

Properties of Parallelogram

A quadrilateral can be considered as parallelogram when it satisfies certain properties which are mentioned as follows: 

• A parallelogram has facing sides that are parallel to each other.
• A parallelogram has facing sides that are equal to each other.
• The angles opposite to each other are equal in a parallelogram.
•  The two diagonals bisect each other in a parallelogram.
• The sum of same-side interior angles of a parallelogram is 180 degrees.